Afm Unit 2 Review Probability Answers There Are 9 Students Participating

• Inquiry
• Open up Access
• Published: 12 September 2018

Estimating the minimum number of opportunities needed for all students to achieve predicted mastery

Smart Learning Environments book v, Article number:15 (2018) Cite this commodity

• 2339 Accesses

• three Citations

• Metrics details

Abstract

We accept conducted a study on how many opportunities are necessary, on average, for learners to accomplish mastery of a skill, also called a knowledge component (KC), as defined in the Open Learning Initiative (OLI) digital courseware. The study used datasets from 74 different course instances in four topic areas comprising 3813 students and 1.2 million transactions. The analysis supports our claim that the number of opportunities to achieve mastery gives usa new information on both students and the development of class components. Among the conclusions are a minimum of seven opportunities are necessary for each knowledge component, more if the prior noesis amid students are uneven inside a course. The number of KCs in a class increases the number of opportunities needed. The number of opportunities to accomplish mastery can be used to identify KCs that are outliers that may be in demand of ameliorate explanations or further instruction.

Introduction

When designing a new grade or improving an existing course, in that location is a need to estimate the number of do opportunities minimally needed to use prediction models to effectively predict student mastery of the learning objectives and skills. Estimates range from a minimum of two questions for a hidden Markov prediction model (Bier, Lip, Strader, Thille, & Zimmaro, 2014) to four questions for a Bayesian Knowledge Tracing (BKT) prediction model (Bakery, R. S. J., personal communication, January 15, 2015). However, more empirical evidence is needed to meliorate understand how many questions, or practice opportunities, are needed to allow all students to accomplish predicted mastery. Creating validated questions is fourth dimension consuming, in that location are estimates of on boilerplate one hour per problem (Piasentin, 2010). Oftentimes limited resources crave course designers to make tradeoffs in terms of the number of activities and assessment questions they can develop when designing a new grade or revising an existing course. For example, The Raccoon Gang (2018) estimates that it takes 100–160 h to produce one hour of ready online learning content. Therefore, it is essential not to waste resource on developing questions that are not needed, while even so assuring that the learners volition not run out of problem opportunities.

The Open Learning Initiative (OLI), an open educational resources project initiated at Carnegie Mellon University (CMU) and now too housed at Stanford University, creates innovative online courseware and conducts research to improve learning and transform higher educational activity. OLI has begun some initial explorations into using basic Bayesian hierarchical models to predict student mastery (Bier et al., 2014) where learning objectives are defined for each course and are and then cleaved down into skills (also called cognition components, or KCs). Learning objectives place what a student will be able to do or know at the end of an instructional unit. Skills define the sub-objective, or knowledge component, that comprise a given learning objective. Students' mastery of skills are tested through the problems students answer in the digital courseware. All answers are logged. A predictive learning model is then used to determine when each pupil achieves mastery of each learning objective. In general, predictive learning models are used in learning analytics to predict how well students take mastered a skill, cognition component, or concept. Historically, OLI has used a Bayesian hierarchical statistical model. The model used students' responses to previous questions to predict students' learning states (learned or unlearned) for a given skill just did not account for guessing (correctly answering a question when the student does non know the skill) or slipping (incorrectly answering a question when the student does know the skill). Theoretically, learners in OLI courses would non necessarily have to respond all bug, just a sufficient number to make information technology probable they have understood a concept. However, OLI courses do not provide students with a path for moving on afterwards they had mastered a skill, either through a forced pathway or past providing data to the student that she had mastered the skill. The OLI prediction model had a congenital-in assumption that a minimum of ii practice opportunities were needed to effectively make up one's mind if a student had mastered a skill.

It is however not clear how many opportunities are sufficient in general. We can wait that the number will vary amongst different KCs, learners and courses, but how much, and how much is the variance? This information could inform grade designers. What is the optimal number of problems needed to preclude students from running out of problems practise opportunities before they take mastered a skill while at the same time non spending too many resources on developing bug. This paper will explore what is the minimum number of practise opportunities needed to predict mastery for OLI courses that use a basic Bayesian hierarchical statistical model. Additionally, nosotros will explore whether the minimum number of practice opportunities varies by course content or by level of institution.

Groundwork

Our ability to retain a piece of data improves with repeated exposure and decays with delay since the last exposure (Reddy, Labutov, Banerjee, and Joachims, 2016). Continual repetition commonly eventuates in diminished returns (Chen & Squire, 1990; Miller, 1978). To support long-term retention, more practice is necessary but needs to be spread out on an optimal schedule (Anderson et al., 1999; Pavlik & Anderson, 2005). However, for initial learning, more practice becomes over-practice, and one time learned, there are also downsides with continued repetition and might even exist detrimental under certain conditions. Retentiveness for repeated items turn down with increased repetition under incidental-learning conditions (English & Visser, 2013). Response times were significantly longer when a category was repeated aloud for thirty due south, equally compared to only three seconds (Smith, 1984). This decline in performance with prolonged rehearsal was termed the massed repetition decrement (Kuhl & Anderson, 2011).

One of the downsides of too much repetition is the time it takes from other school subjects and social life. Students who do more than hours of homework experience greater behavioral engagement in school but also more bookish stress, physical wellness problems, and lack of balance in their lives (Galloway et al., 2013). Many teachers believe that giving students more practice problems is beneficial and "would like to have the students piece of work on more than exercise problems", fifty-fifty when "[students] were non making any mistakes and were progressing through the tutor quickly" (Cital, 2006 in Cen, Koedinger & Junker, 2007).

Withal, it is possible to reduce study fourth dimension without loss of learning. In a study of high school students participating in the Optimized Cognitive Tutor geometry curriculum, it was constitute that 58% out of 4102 practices and 31% of 636 practice questions were washed after the students had reached mastery (Cen et al., 2007). Results were compared to students participating in the traditional Cognitive Tutor geometry curriculum. Analyses indicated that students in the optimized condition saved a significant amount of time in the optimized curriculum units, compared with the time spent by the control group.

OLI evaluations have investigated the effectiveness of both stand-alone (completely online) and hybrid (supplemented with teacher interaction) compared to traditional instruction. Almost remarkable is a study on Statistics students who learned a full semester'due south worth of material in half the time while performing as well or better on tests and final test compared to students learning from traditional pedagogy over a total semester (Lovett et al., 2008).

Online instruction thus can surpass traditional education in efficiency, but to do this, online systems also requires a lot of practice problems and these tin be resource demanding to construct and verify. There are generic means to define certain problems so that the possibility of running out of problems volition, in do, never occur (Bälter, Enström, and Klingenberg, 2013). Nonetheless, these generic ways require possibilities to ascertain questions and answers from a set of variables. The question and its answers need to exist programmed. These features are rare in near learning management systems, which make the number of problems necessary to construct an important factor when developing new courses. Additionally, the OLI courses are designed to support scaffolded learning focused on conceptual understanding not procedural repetition. Therefore, problems with randomly generated values for a given prepare of variables that require calculations to answer do not fit the learning objectives for nigh OLI courses.

In society to use the data stream from online learning environments to estimate learning we need a theoretical model of learning. We, equally many others, begin with learning objectives that precisely specify the skills and competences needed to be mastered past the learner. Such learning objectives are crucial for both the pattern procedure of effective education, on the one hand, and the assessment of the learning result (i.e., skills and competences), on the other hand (Marte et al., 2008). A further extension is to presume dependencies between the skills, (e.g. Korossy, 1999), inducing a competence structure on the set of skills, just this is not in use (withal) in OLI. A comprehensive review and evaluation of existing frameworks for teaching, learning and thinking skills is provided in a report by Moseley et al. (2004). There are too means to use statistical modeling to create a skills map that reportedly outperforms human experts (Matsuda et al., 2015).

The Bayesian hierarchical learning model used to predict mastery of skills and learning objectives in OLI courses assumes a ii-state learning model. Learners are either in the learned or unlearned land for a given skill. Students can transition from unlearned to learned state at each opportunity to practice that skill (typically by answering a question on the skill). Subsequently each opportunity, the model estimates the probability that the student has learned the skill (p(Fifty)). At each opportunity, the judge for p(L) is updated based on whether the educatee answered the question correctly or incorrectly (Corbett & Anderson, 1994).

OLI courses contain two types of opportunities: formative assessment questions embedded throughout a module where students can answer the questions multiple times with immediate feedback given afterward each try and summative assessment questions at the end of a department module that act as "quizzes" or "checkpoints" before the pupil progresses to the side by side department or module. All opportunities are equally weighted in the OLI predictive learner model. The OLI predictive learner model uses only the student's first effort at answering the problem as this is considered the most honest attempt. The rationale for this is that the OLI system provides immediate feedback to all determinative assessment questions so later answering a question for the commencement time students tend to click through all the reply choices and review the feedback for each. Lastly, the model used in OLI assumes that once a pupil learns the skill she cannot transition back to the unlearned land (i.east., there is no parameter for forgetting in the model).

OLI has contributed much of its data to the Pittsburgh Science of Learning Center's DataShop (http://pslcdatashop.org/), a central repository to store research data that also includes a set of assay and reporting tools. In 1 of its standard reports, DataShop provides "predicted learning curves" which are the average predicted mistake of a knowledge component over each of the learning opportunities. Learning curves as a method to explain user-computer interaction evolved out of the work of Newell & Rosenbloom (1981). They demonstrated how learning is a power office based on the number of trials at practicing a skill. The greatest learning on a skill occurs early and lessens with additional practice (Newell & Rosenbloom, 1981). Nonetheless, Anderson et al. (1989) found that this power relationship may not always hold truthful with complex skills. In general, learning curves can be used to demonstrate students' learning rates over repeated trials practicing a skill (Koedinger & Mathan, 2004).

Other models

A full background on learning models is beyond the telescopic of this paper. However, below we present a cursory clarification of other learning models to demonstrate alternate options for predicting student mastery. Additionally, we recognize the prediction model currently used in OLI courses does non reverberate recent advances in learner modeling and equally a effect may introduce fault into the modeling of noesis components.

Other predictive learning models that take been developed are extensions of or new approaches to predicting educatee mastery. These models are used to predict the probability that a educatee tin can answer the adjacent question on a given skill correctly and use a binary upshot for correctness (correct or incorrect). An supposition underlying these models is that each question involves a single skill (Pardos, Gowda, Baker, & Heffernan, 2012).

Bayesian Noesis Tracing, or BKT, uses a like modeling approach as the Bayesian hierarchical learning model used by OLI in that is includes parameters for prior learning and the transitioning from an unlearned to a learned land, but also includes parameters for guessing (the educatee is in an unlearned state simply correctly answered by guessing) and slipping (the educatee is in a learned state just incorrectly answered due to making a fault) (Corbett & Anderson, 1994). This standard BKT model uses skill-specific parameters. Yudelson, Koedinger, and Gordon (2013) discovered that including student-specific parameters, specifically speed of learning, improved mastery prediction compared to the standard BKT model. Lee & Brunskill (2012) used educatee-skill pairs to build an individualized model and found that a considerable fraction of students, as judged past individualized model, would have received a significantly different corporeality of practice bug from the Intelligent Tutoring System. Standard BKT models typically crave a minimum of four opportunities per skill (R. S. J. Baker, personal communication, January 15, 2015).

Additive Cistron Models (AFM) is a logistic regression model that includes educatee ability parameters, skill parameters, and learning rates. AFM assumes all students accumulate knowledge in the aforementioned way and disregards the definiteness of individual responses (Chi, Koedinger, Gordon, Jordon, & VanLahn, 2011).

Performance Factors Analysis (PFA) is also a logistic regression model that is an elaboration of the Rasch model based on Item Response Theory. PFA, dissimilar AFM, uses a pupil's number of prior failures (wrong answers) and prior successes (correct answers) on a skill to predict correctness. Unlike BKT, no iterative estimates of latent student knowledge are made merely rather the number of successes and failures are tracked and these are used to predict futurity definiteness (Pardos et al., 2012).

While knowledge tracing (KT), Additive Factor Models (AFM), and Performance Factor Models (PFM) are the three most common educatee modeling methods (Chi et al., 2011), there are other models emerging. A different approach to learning modeling is the use of artificial neural networks. They are usually used to model circuitous relationships between inputs and outputs and to discover patterns in data. Neural networks tin capture nonlinear relationships betwixt concepts, do not require a function to which the data need to exist fitted, and are updated equally more historical data becomes bachelor (Oladokun et al., 2008). Deep Knowledge Tracing (DKT) is a flexible recurrent neural network model that not only predicts students future performance based on their past activity simply also supports selecting the best sequence of learning items to nowadays to a student (Piech et al., 2015).

In addition to BKT, AFM, PFA, and artificial neural network models, other predictive models include linear, Markov, and rule induction models (Zukerman & Albrecht, 2001) every bit well every bit regression, example-based, regularization, conclusion-tree, clustering, deep learning, dimensionality reduction, and ensemble models (Brownlee, 2013). In that location are as well adaptive learning models (Boulehouache et al., 2015) such every bit Felder-Silverman (Kolekar, Pai, & Pai, 2016).

Learning curves and their nomenclature

When asking learners a question on a skill they are learning, instructors aim for many, but not all, of the learners to be able to reply the question correctly. If no one is able to respond the question correctly, it is to a higher place their nowadays abilities, and if anybody can reply information technology correctly it is not worth their endeavour. Regardless what the platonic percentage of right answers for a offset question should be, the learning system should give feedback to individual learners about why their answer was wrong and how they should recall in order to get it right. When that is done correctly, we await for the second question of the aforementioned skill that the percentage of incorrect answers is reduced, meet Fig. 1.

Fig. 1

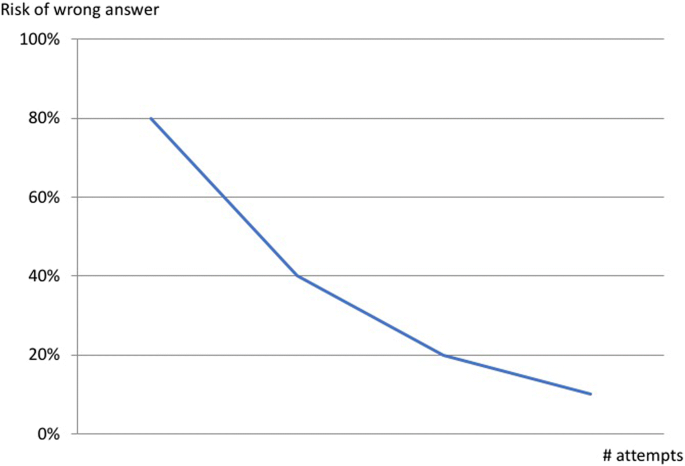
Theoretical learning bend when instructions, questions and feedback are working properly

Full size image

There are many things that can get wrong: the instructions could be hard to interpret, the questions, or their answer alternatives, could be unclear or non realistic, the feedback could exist irrelevant, the sequence of bug could be wrong, the problems could be too difficult or easy, the problems could be measuring a different skill than intended, etc. However, when everything works well, we should be able to meet learning curves like to Fig. 1, and if we do non, we know that the learning textile needs more work.

When interpreting learning curves, a flat high curve indicates students did non learn the skill, a flat depression curve suggests that students already knew the skill and did non need further instruction, and a curve that trends upwards indicates the skill is increasing in difficulty rather than decreasing. Viewing learning curves tin can help brand quick inferences most how well students are learning diverse skills and which skills may need boosted instructional support and/or refinement in how they are assessed (Bakery, 2010).

Subsequently several practice opportunities, nosotros would like the run a risk of a wrong respond to arroyo zero to evidence that the learners accept mastered a skill. However, we need to take into account the possibilities of guesses and slips.. This mastery threshold is by default twenty% in DataShop, where nosotros store and analyze our data sets (Koedinger et al., 2010). DataShop also includes an algorithm categorizes learning curves. If a curve is depression (below the 20% threshold) and flat, information technology indicates that students had mastered that skill already when the course began or that they overpracticed. If the final point of the curve is to a higher place the high error threshold (40% is default), and then the curve is still high. If the slope of the predicted learning curve (as adamant by the Additive Factor Model (AFM) algorithm) is shut to zero (absolute value below 0.001 every bit default), then the curve shows no learning. All KCs that do non fall into whatsoever of the above "bad" or "at risk" categories are considered "practiced" learning curves in the sense that they appear to indicate substantial student learning (PSLC DataShop, 2015). This classification is simply done on KCs that accept a sufficient number of students (10 is default) and opportunities to reply (3 is default).

Methods

This written report addresses the post-obit research questions:

• What is the minimum number of practice opportunities needed to predict educatee mastery of skills?

• Does the minimum number of exercise opportunities vary by course content (Statistics, Biology, Engineering Statics, and Psychology)?

• Does the minimum number of exercise opportunities needed to predict mastery vary by level of institution (Associate'south, Baccalaureate, Master's and Doctoral colleges/universities)?

We used OLI datasets stored at the Pittsburgh Science of Learning Center (PSLC) DataShop from iv unlike OLI topic areas: CC-Statistics Spring 2014, OLI Biological science: ALMAP spring 2014, OLI Engineering Statics - Fall 2011 - CMU and OLI Psychology MOOC GT - Bound 2013 (100 students) (Koedinger et al., 2010).

The statistics dataset comprises student data from instructors who taught with the OLI Probability & Statistics form in the spring 2014 term (January–May, 2014). This grade introduces students to the bones concepts and logic of statistical reasoning and gives the students introductory-level practical power to cull, generate, and properly interpret appropriate descriptive and inferential methods. In addition, the course intends to aid students gain an appreciation for the diverse applications of statistics and its relevance to their lives and fields of study. The class does not assume whatsoever prior knowledge in statistics and its simply prerequisite is basic algebra.

The biology dataset comprises educatee data from instructors who taught with the OLI Introduction to Biology course in the spring 2014 term (Jan–May, 2014). This introductory course defines biology and its relationship to other sciences. The course examines the overarching theories of life from biological research and also explore the fundamental concepts and principles of the study of living organisms and their interaction with the environment. The course examines how life is organized into hierarchical levels; how living organisms use and produce energy; how life grows, develops, and reproduces; how life responds to the surround to maintain internal stability; and how life evolves and adapts to the environment.

The engineering statics dataset comprises student data from instructors who taught with the OLI Technology Statics grade in the fall 2011 term (Baronial–December 2011). Statics is the study of methods for quantifying the forces between bodies. Forces are responsible for maintaining balance and causing motility of bodies, or changes in their shape. You run into a nifty number and multifariousness of examples of forces every day, such as when you press a button, turn a doorknob, or run your hands through your hair. Motion and changes in shape are critical to the functionality of man-made objects as well equally objects the nature. This course uses algebra and trigonometry and is suitable for apply with either calculus- or not-calculus-based academic statics courses. Completion of a beginning physics course is helpful for success in statics, merely not required. Many key physics concepts are included in this course.

The psychology data set comprises student data from instructors who taught with the OLI Introduction to Psychology class in the leap 2013 term (Jan–May 2013). This grade offers students an engaging introduction to the essential topics in psychology. Throughout this study of homo behavior and the mind, you will gain insight into the history of the field of psychology, as well as explore electric current theories and problems in areas such as cognition, motivation, and wellness. The importance of scientific methods and principles of research design is emphasized throughout this grade and presented in a fashion that volition enrich your study of individuals as thinking, feeling, and social beings.

From each dataset, the transactions with KCs classified as "Good" were selected and exported. Each transaction contained data on anonymous student id, KC name, effort number, and predicted mistake charge per unit and additional information that were not used in this assay.

A Java plan was written to extract information from each student and KC combination how many attempts were necessary to achieve mastery for that KC (i.east. identify the first attempt where the predicted error rate became lower than the mastery threshold of xx% (the amount of error allowed in the prediction of mastery), the default value set in DataShop) and whether the pupil reached mastery or non for each KC. Co-ordinate to DataShop documentation, the xx% threshold comes from Bloom (1968), where he constitute that 20% of students were already attaining mastery levels in their learning without improved learning techniques (Koedinger et al., 2010). This data was later on used to make comparisons of descriptive statistics and conduct two-sample t-tests and ANOVA (ANalysis Of VARiance) tests where appropriate.

Results

Statistics course

For the statistics form, run across Table 1 for a summary, the mean number of attempts to reach mastery over all 45 good KCs was 4.iv with a standard divergence of 4.0 (north = 13,411). We take one outlier at 16.six. This is the KC "pvalueinterp". The second highest at nine.9 is "hyptest-logic". The KC "pvalueinterp" is the skill "Interpreting p-value" and "hyptest-logic" is "Logic of hypothesis testing." Questions related to these two KCs appear extensively in the Inference unit of measurement of the Probability & Statistics course. In particular, the "pvalueinterp" skill involves interpreting p-value results from various types of statistical tests from a s-examination for the population mean to chi-square tests. It could be that interpreting the p-value is not a generalizable skill beyond different contexts only rather is multiple skills and/or requires more practice than less circuitous skills. The same may be truthful for "hyptest-logic" in that the process of hypothesis testing for different statistical tests may be multiple skills that requires boosted practice than less complex skills.

Table 1 Statistics course data summary for the 2014 grade

Full size tabular array

If we reduce the mastery limit to 10% and utilize the same 45 KCs we become a slight increase, with a mean of five.0 and a standard deviation of iii.7 (n = 5196). We nonetheless take one outlier at 15.1 which is all the same the KC "pvalueinterp". The second highest at 10.7 is "probtools" (Probability tools) and 10.iv is "samplespace" (Identifying sample infinite). The previously second highest "hyptest-logic" is at present at 5.8.

Nosotros can split the students into students attention 2-year colleges and four-year colleges and their means and standard deviations are shown in Tabular array two. Equally expected the hateful is lower for the four twelvemonth colleges.

Table 2 Hateful number of attempts for two and four year colleges

Total size tabular array

A Welch Two Sample t-test on these two groups gives t = 11.735, df = 3096.viii, p-value < 2.2e-16, 95% confidence interval: 1.0–i.four. If we only compare the mean values for each KC, nosotros go far a Two Sample t-test, t = 2.2705, df = 87, p-value < 0.013, with hateful values vi.i for two twelvemonth colleges and four.one for four year colleges.

A Welch Two Sample t-exam gives a similar p-value: (t = 2.2523, df = 56.966), p-value < 0.014.

We take, besides "pvalueinterp" at 36 and "hyptest-logic" at 17, three loftier values for the two-year colleges. These are the KCs "ztestcond" (Weather of z-test and t-examination), "translate-probdist" (Application of probability distribution) and "probtools" (Probability tools). The KC related to identifying conditions for when to use a z-test and t-test is the showtime major topic in the Inference department of the OLI Probability & Statistics course. Students who have had no prior feel with statistics, which is often the case at two-twelvemonth colleges, tend to struggle when in the showtime office of the Inference unit. Also, two-year college students tend to have less background noesis in that surface area and then it is not surprising that two of the outliers are related to probability topics.

Equally the means are important for the further discussion, we will not include the two outliers in the analysis below.

Another mode to dissever the colleges is to use "Carnegie Classification of Institutions of Higher Education" (2005). This classifies American colleges and universities into one of 31 groups. For our purpose we need fewer groups and preferably a sorting order. Therefore, nosotros mapped the 23 participating colleges into one of 4 master categories: Associate's, Baccalaureate, Master's and Doctoral colleges/universities. 1 of the participating colleges was Canadian and was classified as a Doctoral university based on information on the number of graduated Ph.D. students on their web page.

In Tables 3 and 4 we can encounter that the hateful drops as expected between Associate's, Baccalaureate/Primary's and Doctoral colleges. The similarities between the Baccalaureate and the Main's higher students may be surprising, but it may be that the student populations at master's-degree granting institutions are like to the student populations at baccalaureate-degree granting institutions in terms of prior knowledge and learning in math and statistics making these two classifications indistinguishable from one some other in terms of student performance on these skills.

Table three Mean number of attempts for associate'south, baccalaureate, master's and doctoral colleges with two troublesome KCs removed

Full size table

Table 4 Mean number of attempts for Associate'southward, Baccalaureate, Master'south and Doctoral colleges with mastery limit set at x% and the two (20%) troublesome KCs removed

Full size tabular array

An ANOVA followed by a Tukey multiple comparisons of means at 95% family-wise confidence level comparison the 3 different higher levels (Associate's, Baccalaureate/ Master'due south and Doctoral) confirms that the mean differences of number of attempts needed to attain mastery are statistically significant (p < 0.001) among all 3 weather. The conviction intervals for the differences are shown in Tabular array 5.

Table 5 Hateful differences between Associate's, Baccalaureate, Principal's and Doctoral colleges and confidence intervals

Full size table

There is also an instance of the same course from 2015 with 781 students. There are some differences between the form instances resulting in simply 39 Good KCs for the 2015 data compared to 45 Expert KCs for the 2014 data. The principal alter between the 2014 and 2015 instance is that in the latter additional checkpoint (summative assessment) questions were added to allow for question pools and to address deficiencies in number of questions per skill. While the OLI model equally weights the formative and summative questions, the summative questions tend to be more difficult and conduct higher importance in terms of a student's grade. Using the aforementioned set up of good KCs as in the analyses above (which includes 12 No learning and four Even so high in the 2015 dataset) we get a mean of 4.9, standard deviation of 4.five (Northward = 6212). This is 10% higher than the 2014 dataset, but may exist explained by the inclusion of more difficult checkpoint questions. The 2015 prepare contains the same outliers equally the 2014 gear up.

If we await only at the good KCs in the 2015 dataset, the number of good KCs drops to 39, (see Table 6). The hateful is fifty-fifty higher at 6.2 with a standard deviation of 5.3 (N = 5553). In this dataset "pvalueinterp" and "hyptest-logic" did non fifty-fifty go far into the good KCs. Amidst the highest that did are at "probtools" as usual, but the three next ones are new: "apply_probability_rules_skill", "estimater" and "onevstwosided". Notwithstanding, all four are betwixt 10.vii and 12.2.

Tabular array 6 Statistics course information summary for the 2015 course

Full size table

Comparing the median number of questions per KC in the two statistics datasets (see Table 7) nosotros can see that the median number of problems per KC increased from 5 to 8 across all 107 KCs from 2014 to 2015. For the Expert KCs, the median number of problems increased from five to ix. The median for the All the same high KCs remained relatively flat nigh 6 issues. The "No learning" median increased from 1 to iv.five, only was still half that for the median of the Skilful KCs indicating these KCs demand boosted questions.

Table seven Problems per KC for the 2014 and 2015 Statistics courses

Full size table

Biology form

For the Biology form, see Tabular array 8 for a summary, the hateful was three.1 with a standard departure of iii.6 (N = 6211). There is an outlier named c33 which is a chemical compound of the KCs: _u3_cell_function_explain_somatic_gametes_diff_skill,

_u3_chromosome_structure_describe_per_cell_cycle_skill and.

_u3_chromosomes_nbr_and_structure_per_type_skill. Joining KCs like this might be a skillful idea to reduce the number of necessary test opportunities, just in this particular instance something might have gone wrong and a course designer should take a closer await at this KC. Removing that outlier results in a mean of two.eight and a standard deviation of 3.ane (Northward = 5980).

Table viii Biology course data summary

Full size table

In the Biological science course, all students came from the aforementioned university, which dominion out subdivisions. However, there are several noesis models bachelor that vary the number of estimated KCs and if nosotros use Model1 with 50 good KCs, we get a mean of 2.9 and a standard deviation of 2.1. There are no outliers for Model1. As expected, the number of attempts needed per KC drops when the number of KCs increment. However, the total number of attempts to achieve mastery increment from 6211 to 12,089, that is, in this case when the number of KCs increased by a factor 2 (from 25), so did the number of attempts necessary to reach mastery.

Engineering statics course

For the Engineering Statics form, see Table 9 for a summary, the mean was five.3 with a standard divergence of 4.half dozen (Northward = 2152). There is an outlier with 14.iv attempts on average "couple_represents_net_zero_force". Removing that outlier results in a mean of 4.6 with a standard deviation of 4.0 (N = 2014).

Table nine Technology statics course information summary

Full size table

If we reduce the mastery limit to ten% in the Engineering Statics class, with the same outlier removed, the mean increases to 8.i with a standard deviation of 5.0 (N = 948). Compared to the minimal differences in other courses, this grade is deviating from the pattern. Ane explanation is that information technology is a more advanced course. In contrast to the other courses, it has recommended (not required) prerequisites which not all students may take fulfilled, resulting in more than do issues needed to reach mastery with the limit set to ten%.

Psychology course

Due to the size of the dataset, the Psychology course, see Table ten for a summary, is divided in three unlike datasets with no overlap of students to go far possible for the server to compute the learning curves. We tried to use a supercomputer with 50GB of retention to exist able to include the entire prepare, merely to no avail. Due to random differences between students in these sets, the learning curves and classifications accept minor differences betwixt the sets. We used the KCs classified as Good in the largest of these iii sets on the other ii sets as well.

Table 10 Psychology class data summary

Full size table

For the Psychology course the hateful was 3.nine with a standard difference of 3.9 (N = 32,355). There is an outlier "physical_psychological_changes_adulthood" at sixteen.9. Removing that outlier results in a mean of 3.7 with a standard deviation of three.5 (Northward = 31,907).

For this course nosotros also have admission to results on the concluding exam. The Pearson's product-moment correlation between the students' number of attempts and the event of the final test is shown in Table eleven. All correlations are weak, but in the expected directions: the fewer attempts needed to master all skills (lower hateful and median), the better result on the final examination. Also, the more than KCs mastered, the better result on the final examination and the lower standard departure, the amend consequence. A scatterplot over attempts vs. final test score is illustrated in Fig. ii.

Table eleven Correlations between number of attempts and concluding examination score

Full size table

Fig. 2

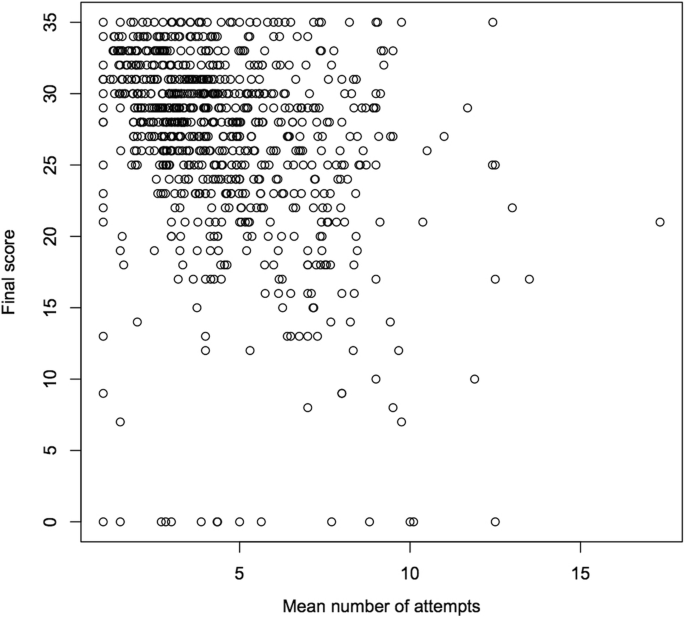
Scatterplot over the mean number of attempts and final test score

Full size image

If we look but at the nearly hard KCs (ten highest hateful number of attempts) the correlation is somewhat stronger (mean − 0.36, median − 0.38) which is confirmed in the scatterplot in Fig. 3.

Fig. three

Scatterplot over the mean for the top ten KCs and final test score

Total size image

All these students had finished the course in that sense they have a score on the final exam. If the KCs that crave a high number of attempts had been unevenly distributed, for example most in the beginning, and low achieving (in terms of score on terminal exam) students stopped answering the online questions, that could explain the correlations above. Nevertheless, as tin can exist seen in Fig. 4, the distribution of high enervating and depression enervating KCs is pretty even over the course.

Fig. 4

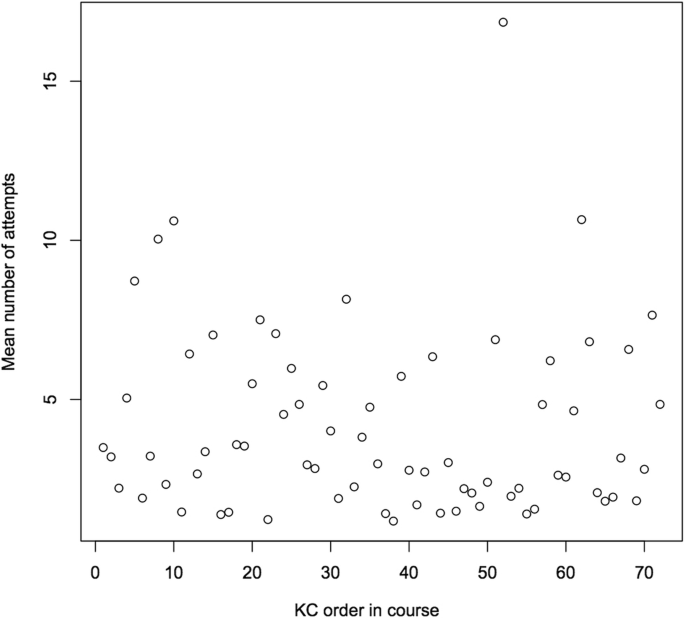
Distribution of mean number of attempts over the course

Total size epitome

Word

Nosotros accept performed a study of the number of opportunities necessary to reach mastery for four different college level courses. Although there are differences, these differences are modest between KCs, student groups, and colleges. So, how many opportunities are enough to predict pupil mastery?

Ideally, an online grade should never run out of questions for the learners as this would prevent some learners from mastering certain skills. However, speaking informally with students almost this, there is an credence for new systems to non be perfect in this sense equally long as this only occur occasionally. This acceptance is vital, because creating validated questions is time consuming, nosotros estimate this to on average, one hour per problem (Piasentin, 2010), and this should be multiplied with the number of KCs for a course, making every extra question resource demanding. One time the course is up and running, troublesome KCs tin be identified and extra questions for these can be added, simply for new courses a rule of thumb could be helpful to get the course practiced plenty without draining resources.

From Table 12 which summarize our findings we can run across that the mean number of attempts to reach mastery is somewhere between 3 and half dozen (with two exceptions discussed below), with a standard deviation between 3 and 5. These histograms generally follow a lognormal distribution in that the information skews towards very large positive values (Damodaran, n.d.). However, since the mean and standard departure of the sample are bachelor we can guess μ* (log hateful) and σ* (log standard deviation) of the lognormal distribution. For the hateful, μ* equals x-bar / √ω and σ* equals exp.(√(log(ω)) where ω equals 1 + (s / x-bar)² (Limpert et al., 2001). The log mean plus ii standard deviation covers 98% of the students' needs for opportunities. In the end, it is up to the course designers to determine what the coverage should be and how much resources can be used for questions, just equally a dominion of thumb: effectually vii questions. This can exist compared to the median 8 questions bachelor per KC beyond all 107 KCs in the 2015 Statistics course and a median of ix questions per KC for those classified as "Proficient." In dissimilarity, some of the problematic KCs showed fewer opportunities such as the 7 out of 107 KCs that were classified as "Yet high" (median six opportunities per KC) and four others as "Too piddling data" (median 4.5 opportunities per KC).

Table 12 Comparison between mean, standard deviation and log mean + 2SD for all subgroups

Full size table

Where nosotros accept identified outliers we have removed them. The reason is that identifying outliers in this manner is a fashion of identifying parts of a course that demand an overhaul. We do non believe that it is optimal for the learners to usually reach mastery in 4–v attempts and suddenly need 15, and these are the averages, for some learners these numbers are much higher.

Despite all the manipulations with dissimilar students, courses, number of KCs and mastery thresholds, the hateful values in number of attempts to reach mastery varied very picayune except in one form, the Engineering Statics course. While the furnishings of the mean for the statistics course increased less than an attempt when the level of mastery was halved from 20% to x%, on the Engineering Statics course the hateful almost doubled. We can therefore non state that the number of attempts is independent of the mastery threshold for an advanced course that has recommended prerequisites.

As expected, the number of attempts needed drops when the number of KCs increment. In this case when the number of KCs increased by a gene of two, then did the number of attempts necessary to accomplish mastery. More than KCs means more questions for students to answer, but the questions are "easier" for students to primary because the concept existence covered in each question is smaller in scope. If nosotros strive for efficiency in our courses, nosotros should therefore as well strive for a remainder between the number of KCs and number of questions we pose. Fewer KCs results in more questions necessary on the same (aggregated) skill, while more KCs lead to more questions in total. As nosotros could see in this case, too few KCs may as well lead to as well complex questions causing outliers amidst the questions.

In the Psychology form we were able to compare the number of attempts needed to achieve mastery with the results on a written final exam. The statistical analyses point in the same direction: the number of attempts is indicative of the students' learning land (as measured by the exam).

A limitation of this report is the somewhat arbitrary threshold for mastery. As the true learning state of a pupil is non possible to determine we are confined to indirect methods such equally asking questions.

Could this be generalized to other courses? Possibly, as the bridge of courses in this study cover four different subjects with rather small-scale differences, with the ane exception mentioned to a higher place. Still, out of necessity all courses in this report are OLI courses, and the lack of differences might exist an upshot of the methods to create and implement OLI courses.

Could this be generalized to other students? All students in this study are adults so the validity of this study for Chiliad-12 pedagogy is limited. However, the differences between the different students groups we could extract (two vs four year colleges; Acquaintance's, Baccalaureate, Master'south and Doctoral colleges) are small. It would not be surprising if a study on loftier school students would show similar results. However, such studies must exist done on courses intended for that age group, which the present OLI courses are not, but we are investigating other possibilities to reach downwardly in age.

Conclusions

The number of opportunities necessary to reach mastery on OLI courses differs very little betwixt the iv dissimilar courses examined and also between different types of college students. For other researchers and teachers who are developing online courses we would recommend offering at least seven opportunities to examination each skill, more if the form is advanced and the prior knowledge among the students may exist uneven. An upper limit is a thing of resource, but these are better spent on identifying high demanding skills to either add together more opportunities there, or to empathise why those specific skills are and so much more difficult to master and possibly improve the instructions.

Nosotros accept observed a natural linear relation between the number of KCs and number of attempts necessary to attain mastery in full. However, this is only based on a unmarried course and more studies are needed to validate this.

The algorithms for classifying learning curves could be refined to detect outliers among the KCs. We believe KCs with a high number of opportunities needed to master them should exist farther investigated to empathise why those detail skills are so difficult to master. It might be something wrong with the instruction. Even if there is nothing wrong, those skills take the largest potential of improvement in our goal to make learning every bit efficient as possible.

Abbreviations

AFM:

Condiment Factor Models

ANOVA:

ANalysis Of VARiance

BKT:

Bayesian Knowledge Tracing

CMU:

Carnegie Mellon Academy

DKT:

Deep Knowledge Tracing

KC:

Knowledge Component

KT:

Knowledge Tracing

OLI:

Open Learning Initiative

PFA:

Performance Factors Analysis

SD:

Standard Deviation

References

• J.R. Anderson, F.G. Conrad, A.T. Corbett, Skill acquisition and the LISP tutor. Cogn. Sci. 13(4), 467–505 (1989)

  Commodity  Google Scholar

• J.R. Anderson, J.M. Fincham, S. Douglass, Do and retention: A unifying analysis. J. Exp. Psychol. Learn. Mem. Cogn. 25, 1120–1136 (1999)

  Article  Google Scholar

• R.S.J. Baker, in Advances in intelligent tutoring systems. Mining information for educatee models (Springer, 2010), pp. 323–337

• O. Bälter, E. Enström, B. Klingenberg, The event of short formative diagnostic web quizzes with minimal feedback. Comput. Educ. 60(1), 234–242 (2013)

  Article  Google Scholar

• Bier, N., Lip, S., Strader, R., Thille, C., & Zimmaro, D. (2014). An Approach to Cognition Component / Skill Modeling in Online Courses. Open Learning, (April), 1–14

• B.S. Bloom, Learning for mastery. Instruction and curriculum. Regional education Laboratory for the Carolinas and Virginia, topical papers and reprints, number one. Evaluation Comment 1(2), n2 (1968)

  Google Scholar

• S. Boulehouache, R. Maamri, Z. Sahnoun, A component-based cognition domain model for adaptive human learning systems. Int J Cognition Learning 10(4), 336–363 (2015)

  Article  Google Scholar

• Brownlee, J. (2013). A bout of motorcar learning algorithms. Retrieved September vii, 2018, from http://machinelearningmastery.com/a-tour-of-machine-learning-algorithms/

• Cen, H., Koedinger, K. R., & Junker, B. (2007). Is over do necessary? Improving learning efficiency with the cognitive tutor through educational data mining. Proceedings of the 13th International Conference on Artificial Intelligence in Instruction AIED 2007, 158, 511–518. Retrieved from http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.i.142.7340&rep=rep1&type=pdf

• K.South. Chen, Fifty.R. Squire, Strength and duration of word-completion priming as a function of give-and-take repetition and spacing. Bull. Psychon. Soc. 28(2), 97–100 (1990)

  Commodity  Google Scholar

• Grand. Chi, K.R. Koedinger, G.J. Gordon, P. Jordon, K. VanLahn, in Proceedings of the 4th International Conference on Educational Data Mining, ed. by M. Pechenizkiy, T. Calders, C. Conati, South. Ventura, C. Romero, J. Stampe. Instructional factors assay: A cognitive model for multiple instructional interventions (2011), pp. 61–70

  Google Scholar

• Carnegie classification of institutions of higher teaching (2005). Retrieved September 7, 2018 from http://carnegieclassifications.iu.edu/definitions.php

• A.T. Corbett, J.R. Anderson, Knowledge tracing: Modeling the conquering of procedural knowledge. User Model. User-Adap. Inter. 4(4), 253–278 (1994)

  Article  Google Scholar

• Damodaran, A. (north.d.). Statistical distributions. Retrieved September 7, 2018, from http://people.stern.nyu.edu/adamodar/New_Home_Page/StatFile/statdistns.htm

• One thousand.C.W. English, T.a.W. Visser, Exploring the repetition paradox: The effects of learning context and massed repetition on memory. Psychon. Bull. Rev. 21(4), 1026–1032 (2013) https://doi.org/x.3758/s13423-013-0566-1

• Thou. Galloway, J. Conner, D. Pope, Nonacademic effects of homework in privileged, loftier-performing high schools. J. Exp. Educ. 81(iv), 490–510 (2013) https://doi.org/10.1080/00220973.2012.745469

• Koedinger, K. R., Baker, R. Sj., Cunningham, K., Skogsholm, A., Leber, B., & Stamper, J. (2010). A data repository for the EDM community: The PSLC DataShop. Handbook of Educational Data Mining, 43

• Koedinger, Thousand. R., & Mathan, South. (2004). Distinguishing qualitatively different kinds of learning using log files and learning curves. In ITS 2004 Log Analysis Workshop (pp. 39–46)

• S.V. Kolekar, R.M. Pai, M.M.K. Pai, Clustering learner profiles based on usage data in adaptive e-learning. Int J Knowledge Learning 11(1), 24–41 (2016)

  Google Scholar

• Korossy, K. (1999). Modeling Noesis every bit Competence and Performance. Knowledge Spaces: Theories, Empirical Inquiry, and Applications, 103–132

• B.A. Kuhl, Thou.C. Anderson, More is not always better: Paradoxical effects of repetition on semantic accessibility. Psychon. Balderdash. Rev. 18(5), 964 (2011)

  Article  Google Scholar

• Lee, J. I., & Brunskill, E. (2012). The Impact on Individualizing Pupil Models on Necessary Practice Opportunities. International Educational Information Mining Social club

• E. Limpert, Westward.A. Stahel, One thousand. Abbt, Log-normal distributions beyond the sciences: Keys and clues on the charms of statistics, and how mechanical models resembling gambling machines offer a link to a handy manner to characterize log-normal distributions, which tin provide deeper insight into va. BioScience 51(5), 341–352 (2001)

  Commodity  Google Scholar

• M. Lovett, O. Meyer, C. Thille, The open learning initiative: Measuring the effectiveness of the OLI statistics course in accelerating student learning. J. Interact. Media Educ. 2008(1), 1–16 (2008) https://doi.org/http://doi.org/10.5334/2008-xiv

• B. Marte, C.M. Steiner, J. Heller, D. Albert, Activeness-and taxonomy-based knowledge representation framework. Int J Knowledge Learning iv(2–three), 189–202 (2008)

  Article  Google Scholar

• North. Matsuda, T. Furukawa, N. Bier, C. Faloutsos, in Proceedings of the 8th International Briefing on Educational Data Mining. Car beats experts: Automatic discovery of skill models for information-driven online course refinement (2015), pp. 101–108

  Google Scholar

• Yard.A. Miller, in Linguistic Theory and Psychological Reality, ed. by M. Halle, J. Bresnan, Grand. A. Miller. Semantic relations amongst words (MIT Press, Cambridge, MA, 1978), pp. 60–117

  Google Scholar

• D. Moseley, V. Baumfield, S. Higgins, M. Lin, J. Miller, D. Newton, et al., in ERIC. Thinking skill frameworks for Post-sixteen learners: An evaluation. A research report for the learning and skills research Center (2004)

  Google Scholar

• A. Newell, P.South. Rosenbloom, Mechanisms of skill conquering and the law of exercise. Cognitive Skills and Their Acquisition 1, i–55 (1981)

  Google Scholar

• V.O. Oladokun, A.T. Adebanjo, O.Eastward. Charles-Owaba, Predicting students' academic functioning using artificial neural network: A case written report of an engineering science course. The Pacific Periodical of Science and Technology ix(1), 72–79 (2008)

  Google Scholar

• Z.A. Pardos, S.M. Gowda, R.S. Bakery, Due north.T. Heffernan, The sum is greater than the parts: Ensembling models of student knowledge in educational software. ACM SIGKDD Explorations Newsletter 13(2), 37–44 (2012)

  Commodity  Google Scholar

• P.I. Pavlik, J.R. Anderson, Practice and forgetting effects on vocabulary memory: An activation-based model of the spacing upshot. Cogn. Sci. 29(iv), 559–586 (2005)

  Article  Google Scholar

• K.A. Piasentin, Exploring the optimal number of options in multiple-choice testing. Council on Licensure, Enforcement and Regulation (CLEAR) Examination Review 21(1), 18–22 (2010)

  Google Scholar

• C. Piech, J. Bassen, J. Huang, S. Ganguli, M. Sahami, L.J. Guibas, J. Sohl-Dickstein, Deep knowledge tracing. Adv. Neural Inf. Proces. Syst., 505–513 (2015)

• PSLC DataShop. (2015). Retrieved September 7, 2018, from https://pslcdatashop.web.cmu.edu/help?page=learningCurve#viewing

• Due south. Reddy, I. Labutov, South. Banerjee, T. Joachims, in Proceedings of the 22Nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (Pp. 1815–1824). Unbounded human learning: Optimal scheduling for spaced repetition (ACM, San Francisco, California, Usa, 2016) https://doi.org/10.1145/2939672.2939850

• L.C. Smith, Semantic satiation affects category membership decision fourth dimension only not lexical priming. Mem. Cogn. 12(v), 483–488 (1984)

  MathSciNet  Article  Google Scholar

• M.5. Yudelson, K.R. Koedinger, G.J. Gordon, in International Conference on Artificial Intelligence in Education. Individualized bayesian cognition tracing models (Springer, 2013), pp. 171–180

• I. Zukerman, D.W. Albrecht, Predictive statistical models for user modeling. User Model. User-Adap. Inter. 11(ane–ii), 5–18 (2001)

  Article  MATH  Google Scholar

Download references

Acknowledgments

We are grateful for the assistance in accessing and interpreting data nosotros received from Cindy Tipper, Senior Research Programmer, Human-Computer Interaction Establish at Carnegie Mellon University and Norman Bier, Director of the Open Learning Initiative (OLI) and Cadre Collaborations at Carnegie Mellon University.

Funding

This work was partly generously funded by KTH's Resource Centre for Netbased education.

Availability of information and materials

We used the 'CC-Statistics Spring 2014', 'ALMAP spring 2014', 'OLI Engineering Statics - Autumn 2011 - CMU 148 students)' and the 'Psychology MOOC GT - Leap 2013 (100 students)' datasets accessed via DataShop (Koedinger et al., 2010).

Author data

Affiliations

1. Graduate Schoolhouse of Instruction, Barnum Heart, 505 Lasuen Mall, Stanford, CA, 94305-3003, USA

   Olle Bälter & Candace Thille

2. Open Learning Initiative, Barnum Center, 505 Lasuen Mall, Stanford, CA, 94305-3003, United states of america

   Dawn Zimmaro & Candace Thille

Contributions

OB proposed the study, did the majority of the data analysis, wrote most parts of the paper. DZ refined the report suggestion, assisted with the interpretation of data, did parts of the data assay, and wrote large parts of the newspaper. CT inspired and refined the report suggestion and wrote parts of the paper and reviewed and refined the newspaper. All authors read and approved the concluding manuscript.

Corresponding author

Correspondence to Olle Bälter.

Ideals declarations

Competing interests

The authors declare that they take no competing interests.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/past/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided yous requite appropriate credit to the original writer(due south) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Reprints and Permissions

About this article

Cite this article

Bälter, O., Zimmaro, D. & Thille, C. Estimating the minimum number of opportunities needed for all students to achieve predicted mastery. Smart Learn. Environ. 5, fifteen (2018). https://doi.org/10.1186/s40561-018-0064-z

Download citation

• Received: 01 June 2018

• Accustomed: 29 Baronial 2018

• Published: 12 September 2018

• DOI : https://doi.org/10.1186/s40561-018-0064-z

Keywords

• Knowledge component
• Mastery
• Opportunity
• Digital courseware
• Prediction
• Higher students
• Course grooming

baileysqualkinsaid.blogspot.com

Source: https://slejournal.springeropen.com/articles/10.1186/s40561-018-0064-z

Share this post